Wykupienie dostępu pozwoli Ci czytać artykuły wysokiej jakości i wspierać niezależne dziennikarstwo w wymagających dla wydawców czasach. Rośnij z nami! Pełna oferta →
Zacznę od rzeczy bardzo prozaicznej – od sylogizmu, jakim raczy się uczniów lub początkujących studentów:
Wszyscy ludzie są śmiertelni.
Adam jest człowiekiem.
Ściśle myślący człowiek wyciągnie oczywiście wniosek:
Zatem Adam jest śmiertelny.
Ale przedstawmy ten sylogizm poecie. Dla niego co innego będzie ważne. Wniosek oczywisty, czyli nieinteresujący. Śmierć to dramat ludzkiego istnienia. Sylogizm jest środkiem zbyt ubogim, by wyrazić nieuchronność tego dramatu. Dramat śmierci można by przedstawić na przykład w ten sposób:
Zajęta zabijaniem,
robi to niezdarnie,
bez systemu i wprawy.
Jakby na każdym z nas uczyła się dopiero.
Jeżeli dramatu nie da się pokonać, trzeba go przynajmniej oswoić:
Kto twierdzi, że jest wszechmocna,
Sam jest żywym dowodem,
że wszechmocna nie jest.
Nie ma takiego życia,
które by choć przez chwilę
nie było nieśmiertelne.
Śmierć
Zawsze o tę chwilę przybywa spóźniona
Na próżno szarpie klamkę
Niewidzialnych drzwi.
Kto ile zdążył,
tego mu cofnąć nie może.
O ileż więcej powiedziała Wisława Szymborska we fragmentach tego wiersza niż suchy sylogizm Arystotelesa! A jednak sylogizm miał w sobie coś z nieuchronności śmierci:
Jeżeli p, to q,
p.
A więc q.
Skąd ten przymus wynikania? Czy jednak nie może być tak, żeby było „nie q”? Szymborska mogłaby wyrazić swoją myśl na tysiąc różnych sposobów; sylogizm musi się kończyć jednym, i tylko jednym, wnioskiem. Na tym polega poezja wynikania. Gwiazdy mogą się wypalić, wszystkie wiersze ulec zapomnieniu, niebo i ziemia mogą przeminąć, a wniosek sylogizmu i tak będzie ważny.
Wszystkie możliwe kształty
Oczywiście sylogizm jest prymitywną formą poezji wynikania. Sięgnijmy więc po bardziej subtelny przykład. Już Euklides udowodnił, że liczb pierwszych jest nieskończenie wiele; udowodnił – to znaczy podał ciąg wynikań takich, że ostatnim zdaniem łańcucha wynikań było zdanie: „liczb pierwszych jest nieskończenie wiele”. Do dziś rozmieszczenie liczb pierwszych w zbiorze liczb naturalnych pozostaje zagadką. Na podstawie eksperymentów numerycznych wiadomo na przykład, że w miarę posuwania się w ciągu liczb naturalnych liczby pierwsze pojawiają się coraz rzadziej. Ale mimo to jest ich nieskończenie wiele. W 1737 r. Leonhard Euler znalazł związek między występowaniem liczb pierwszych a pewną funkcją, która wyglądała dziecinnie prosto, ale okazała się bardzo bogata w „matematyczną treść”. Złożoność tej funkcji rozpoznał Bernhard Riemann w referacie wygłoszonym z okazji przyznania mu członkostwa Berlińskiej Akademii Nauk. Był rok 1859, ten sam, w którym ukazało się pierwsze wydanie „O pochodzeniu gatunków” Karola Darwina. Funkcja dzeta Riemanna do dziś jest źródłem wielu problemów matematycznych i przedmiotem fascynacji wielu matematyków.
Przyjrzyjmy się jej nieco dokładniej. Wygląda całkiem prozaicznie, jak wiele innych matematycznych formuł:
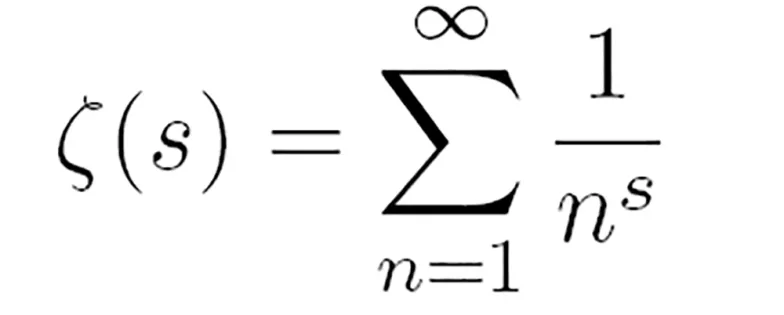
gdzie n jest liczbą naturalną, a s = σ + iτ liczbą zespoloną, której część rzeczywista jest większa od jeden. Nawet jeżeli spojrzeć na tę funkcję „uzbrojonym okiem” matematyka, to trudno w niej dostrzec coś nadzwyczajnego, ale jeżeli uruchomić aparat wynikania, to zaczynają się ujawniać rzeczy zaskakujące. Już Riemann w swojej oryginalnej pracy wysunął hipotezę, że wszystkie zespolone zera funkcji dzeta leżą na prostej σ = 1/2. Mimo niezmordowanych wysiłków, hipoteza ta dotychczas pozostaje nieudowodniona. Na tego, kto przedstawi poprawny dowód, czeka nagroda w wysokości miliona dolarów. Od lat trwają komputerowe próby zmierzenia się z hipotezą Riemanna. Do września 2004 r. sprawdzono 910 miliardów początkowych miejsc zerowych funkcji dzeta oraz kilku miliardów odległych miejsc (w okolicy miejsca zerowego o numerze 1023). Hipoteza Riemanna wyszła z tych prób zwycięsko – nie znaleziono kontrprzykładu. Ale dla matematyków to jeszcze nie dowód; dowód musi posługiwać się „cudem wynikania”, a nie „liczeniem na palcach”, choćby to były „palce” superszybkich komputerów.
Funkcja dzeta Riemanna zaskakuje matematyków swoimi własnościami. Nieustannie są odkrywane nowe, coraz mniej spodziewane. Zaskakuje nie tylko matematyków. W latach 70. ubiegłego stulecia odkryto, że istnieje zbieżność statystycznego rozkładu miejsc zerowych funkcji Riemanna z rozkładem poziomów energetycznych jąder atomowych ciężkich pierwiastków chemicznych. Skąd funkcja dzeta wie o budowie jąder atomowych? Albo odwrotnie: skąd jądra atomowe wiedzą o funkcji dzeta? Przecież funkcja dzeta to czysta matematyka nieskażona żadnymi związkami z doświadczeniem! Czy dotykamy tu jakichś zagadnień mających związek z podstawami naszego rozumienia tych dwu nauk – matematyki i fizyki?
Zostawmy jednak na boku ten pasjonujący problem. Być może jest jeszcze za wcześnie, by go głębiej drążyć. Powróćmy do czegoś, co mamy szansę lepiej zrozumieć.
W 1975 r. Siergiej Michajłowicz Woronin (przedwcześnie zmarły matematyk) udowodnił twierdzenie, znane jako twierdzenie o uniwersalności funkcji dzeta. Mówi ono co następuje:
Rozważmy na płaszczyźnie zespolonej pasek
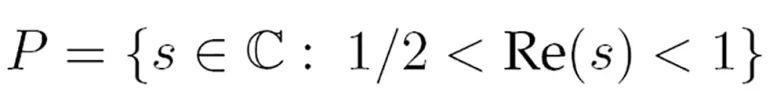
oraz zwarty zbiór U w P, taki, że dopełnienie U jest spójne w P (czyli P nie ma „dziur”). Niech f : U → P będzie funkcją ciągłą na U, holomorficzną wewnątrz U i nieposiadającą miejsc zerowych wewnątrz U.
Twierdzenie Woronina orzeka, że dla dowolnego ϵ > 0 istnieje taka wartość t = t(ϵ), że
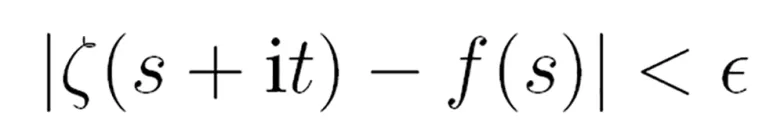
dla każdego s należącego do U.
Twierdzenie to mówi więc, że jeżeli funkcja f przedstawia dostatecznie regularną krzywą, niezerującą się w obszarze, na którym jest określona, to krzywą tę możemy z dowolną dokładnością przybliżać funkcją dzeta Riemanna, przesuwając odpowiednio obszar U wzdłuż osi urojonej.
Jeżeli brzmi to mało poetycko, to wyobraźmy sobie, że zacytowany na początku tego wykładu wiersz Szymborskiej zapisaliśmy pisanymi literami, łącząc je tak, by powstała odpowiednio regularna krzywa. Twierdzenie Woronina stwierdza, że jeżeli odpowiednio przesuniemy obszar U, to funkcja dzeta odtworzy nam wiersz Szymborskiej (z dowolną dokładnością). Okazuje się, że aby odtworzyć wiersz Szymborskiej, musielibyśmy „pojechać” z obszarem U bardzo daleko wzdłuż osi urojonej. Tak daleko, że moc obliczeniowa obecnych, a nawet zapewne przyszłych komputerów jest za mała, aby tam dotrzeć. Ale to w niczym nie zmienia sytuacji, że wiersz Szymborskiej tam jest.
Zagęszczenie treści
Być może tu zaprotestujemy. Nie wiersz Szymborskiej, lecz tylko kształt linii, przy pomocy której ten wiersz został zapisany. Ale czymże innym jest wiersz Szymborskiej, jak nie kształtem, który jakoś rozpoznajemy? Ostatecznie komputery, które tak wiele mogą, także rozpoznają tylko „kształty” zer i jedynek. I nic ponadto.
Dotykamy tu głębokiego problemu filozoficznego: czy istnieje coś oprócz formy, kształtu? Czy to, co nazywamy treścią, nie jest tylko zagęszczeniem formy? W tym także jest poezja, że funkcja Riemanna podprowadza aż pod takie problemy. A przecież Szymborska była tu tylko pretekstem. Równie dobrze zamiast jej wiersza moglibyśmy się posłużyć „Elementami” Euklidesa lub „Dziełami wszystkimi” Szekspira. Musielibyśmy tylko jeszcze dalej przesuwać się wzdłuż osi urojonej.
Jeżeli ktoś jeszcze wątpi w to, że matematyka jest poezją, niech napisze wiersz, poemat, cokolwiek..., w którym zawierałyby się wszystkie utwory poetyckie świata i wszystkie rozprawy naukowe. Jeżeli ideałem poezji jest prostota zapisu przy bogactwie treści, to żaden Szekspir nie napisał nic piękniejszego od funkcji Riemanna.
Stop! Czy nie posunęliśmy się za daleko? Ostatecznie, ściśle rzecz biorąc, funkcja dzeta zawiera tylko wszystkie możliwe kształty. Dobierając odpowiednie parametry s i t, możemy odtworzyć dowolną, odpowiednio regularną krzywą. Czy to aż tak dziwne? Upieram się jednak, że matematyka jest poezją, i to poezją najwyższego lotu.
Poezja próbuje wyrazić Niewyrażalne przy pomocy metafor, rozmycia reguł gramatycznych, nieoczekiwanych kontrastów znaczeń. Matematyka wydaje się prozaiczna, bo w postaci prostych twierdzeń potrafi wyrażać związki, których prawdziwość jest zagwarantowana ciągami kontrolowanych przez nas wynikań. Ale ma również środki, by wyrazić – jak poezja – to, czego nie da się wyrazić w języku innym niż matematyka. Pomyślmy na przykład o różnych twierdzeniach o zmierzaniu do nieskończoności, o twierdzeniach egzystencjalnych, które mówią, że coś istnieje, choć nie potrafimy tego skonstruować, o strukturach – takich jak funkcja Riemanna – zawierających w sobie niewyobrażalnie bogatą treść.
W tym widzę poetyczność matematyki. Ale pomiędzy tym, co tradycyjnie nazywamy poezją, a poezją matematyki, istnieje jedna zasadnicza różnica. W matematyce najbardziej poetyczne jest to, że obowiązuje w niej ścisłe wynikanie. Gdyby tylko w jednym miejscu ono zawiodło, wszystko by się zamieniło w kicz i kupę bzdur.
Jak w dziele sztuki. Michał Anioł miał powiedzieć, że rzeźba jest już w bryle marmuru, trzeba tylko dłutem odrzucić to, co zbyteczne. Z tym że ludzkie dzieła sztuki są niedoskonałe: jedna poprawka za dużo i też mamy dzieło sztuki, tylko trochę gorsze i nigdy nie wiadomo, czy nie mogłoby być lepiej. Poezja matematyki jest doskonała, bo jeżeli dysponujemy dowodem, to wiemy, że jest tak, jak powinno być. ©
KS. PROF. MICHAŁ HELLER jest kosmologiem i filozofem, autorem kilkudziesięciu książek. Laureat wielu nagród i wyróżnień, m.in. Nagrody Templetona (2008). Dyrektor Copernicus Festival.