Wykupienie dostępu pozwoli Ci czytać artykuły wysokiej jakości i wspierać niezależne dziennikarstwo w wymagających dla wydawców czasach. Rośnij z nami! Pełna oferta →
Pojęcie liczby jest niezwykłym osiągnięciem człowieka. Pitagorejczycy mawiali: „liczby są podstawą wszystkiego”, wierząc, że za pomocą proporcji liczb naturalnych można opisać całą rzeczywistość. Gdy odkryto liczby niewymierne, wiara ta załamała się, ale liczby nie przestały być użyteczne i warto było badać ich własności. W szczególności zauważono, że liczb naturalnych jest nieskończenie wiele. Rozumiane jest to w ten sposób, że dla każdej wymyślonej liczby można podać większą. Choć dla nas to oczywisty fakt, trudno wskazać moment w historii, kiedy to zauważono.
Łatwo wypowiada się twierdzenia typu: „takich a takich to liczb jest nieskończenie wiele”, ale jak to rozumieć? Starożytni Grecy wyróżnili dwa typy nieskończoności: potencjalną i aktualną. Ta pierwsza oznacza, że możemy się do niej zbliżać, lecz nie można jej osiągnąć. Na przykład liczb naturalnych jest potencjalnie nieskończenie wiele, ponieważ dla każdej pomyślanej liczby możemy wskazać większą choćby o jeden. Dla Greków prosta też była potencjalnie nieskończona, gdyż w zasadzie był to odcinek, który można było dowolnie przedłużać – w nieskończoność. Natomiast nieskończoność aktualna to, mówiąc nieściśle, taka, którą można „wziąć do ręki” – na przykład cała prosta lub cała płaszczyzna względnie zbiór wszystkich liczb naturalnych. Nieskończoność potencjalna jest bliższa intuicji i zdrowemu rozsądkowi. Czy widział ktoś całą prostą lub płaszczyznę? Czy możemy wypisać wszystkie liczby naturalne, nie mówiąc o całkowitych albo wymiernych? Idee nieskończoności aktualnej odrzucono w starożytności. Jej głównym przeciwnikiem był Arystoteles – jego autorytet zadecydował, że do końca XIX w. unikano tego pojęcia. Dopiero w pracach George’a Cantora nieskończoność aktualna była systematycznie wykorzystywana, za co zresztą krytykowało go wielu matematyków.
Praktycznie nieskończona
Matematycy posługują się liczbami, które moglibyśmy nazwać „praktycznie nieskończonymi” – są tak duże, że umykają naszej wyobraźni, a nawet fizycznej interpretacji.
Takie liczby, korzystając z dobrodziejstwa systemu pozycyjnego, łatwo się zapisuje. Kiedy jednak uznajemy, że liczba jest już niewyobrażalnie wielka? Codzienne doświadczenie pokazuje, że nie radzimy sobie nawet z niezbyt wielkimi liczbami. Używamy terminów „milion”, „miliard”, „bilion” (w zapisie wykładniczym 106, 109, 1012). Gry liczbowe czarują nas milionami, ekonomiści mówią o miliardach, bilion pojawia się już rzadziej (chyba że jest mowa o budżecie amerykańskim, ale angielski termin „bilion” jest odpowiednikiem naszego „miliarda”, co zresztą często prowadzi do nieporozumień). Z liczbami 1015, 1018 czy 1030, jeśli nie jesteśmy fizykami, astronomami lub matematykami, w zasadzie nie mamy już jednak do czynienia. Gdy zapytamy, ile to jest milion czy miliard minut, to nie otrzymamy natychmiast odpowiedzi, a oszacowania będą bardzo różne. Naturalnie nietrudno to policzyć, wykorzystując podstawowe działania arytmetyczne. Kto zgadnie, że milion minut to około 694 dni, czyli nieco mniej niż dwa lata? A miliard minut? To już tysiąc razy więcej, czyli 1902 lata (jeśli nie policzymy dni w latach przestępnych). Można tak ćwiczyć wyobraźnię, zadając podobne pytania, np. jak gruby byłby włos ludzki (ok. 0,1 mm), gdyby go powiększyć milion razy? Albo ile stron znormalizowanego maszynopisu zajmie tekst składający się z miliona liter?
Rekord Archimedesa
Starożytni też zmagali się z ogromnymi liczbami. Już Egipcjanie wymyślili symbol oznaczający milion. W historii matematyki znany jest przypadek Archimedesa, który, wbrew ówczesnemu mniemaniu, że liczba ziaren piasku jest nieskończona, oszacował liczbę ziaren potrzebną do wypełnienia znanego mu Wszechświata będącego wnętrzem kuli o średnicy mniej więcej naszych dwóch lat świetlnych. Uważa się, że jest to największa liczba wykorzystana w starożytności do rozwiązania konkretnego zadania. Moglibyśmy ją przedstawić jako potęgę liczby 10, w której wykładniku mamy ósemkę i szesnaście zer: 1080000000000000000.
Docenimy geniusz Archimedesa, gdy uzmysłowimy sobie, że nie posługiwał się systemem pozycyjnym i nie miał do dyspozycji nazewnictwa wielkich liczb poza miriadami – ówczesnym odpowiednikiem 10 tysięcy. Pokazał, że termin „miriada” wystarczy, żeby opisać liczbę, która ma w zapisie dziesiętnym 80 kwadrylionów zer. Wystarczy miriadę miriad pomnożyć przez siebie miriadę miriad razy, a następnie wynik znów przez siebie miriadę miriad razy. Proste? W głowie się kręci od miriad i liczby zer, ale to przecież maleńki krok w drodze do nieskończoności.
W świecie fizycznym rozważane są ogromne liczby, lecz daleko im do liczby Archimedesa. Tzw. długość Plancka, najmniejsza długość w świecie fizycznym, wynosi około 1,612 x 10-35 m, a czas Plancka 5,39166 x 10-44 s (to najmniejsza jednostka czasu z sensem fizycznym). Przypuszczalny wiek Wszechświata wyrażony w jednostkach, którymi jest czas Plancka, wynosi 1,7049932 x 1062. Czas życia naszego Wszechświata od Wielkiego Wybuchu liczony w bardziej swojskich sekundach wynosi mniej niż 1020 sekund.
Liczba wszystkich cząstek elementarnych w obserwowalnym Wszechświecie obecnie szacowana jest na około 1080. Każda liczba przekraczająca 1080 jest „praktyczną” nieskończonością, gdyż nie ma, przynajmniej na razie, sensu fizycznego.
Archimedes postawił poprzeczkę bardzo wysoko i bardzo długo ustanowiony przez niego rekord nie został pobity. W swoim dziele dawał do zrozumienia, że można tworzyć jeszcze większe liczby, lecz była to już czysto teoretyczna zabawa. Oczywiście od czasu do czasu w rozważaniach pojawiały się duże liczby. Na przykład w legendzie o szachach i ziarnach pszenicy mamy do czynienia z liczbą 264, której zapis w systemie dziesiętnym jest ciągiem dwudziestu cyfr. Jednak w porównaniu z liczbą Archimedesa to karzełek. Tak naprawdę dopiero w XX w. zaczęły pojawiać się w naturalny sposób w rozważaniach liczby olbrzymy. Najwięcej takich gigantów powstało w związku z badaniem własności liczb pierwszych.
Liczby ściśle tajne
Przypomnijmy: liczby pierwsze są to takie liczby naturalne, które mają dokładnie dwa różne dzielniki, siebie samą i jedynkę. Zgodnie z tym określeniem jeden nie jest liczbą pierwszą, gdyż ma tylko jeden dzielnik. Każda liczba naturalna daje się przedstawić jako iloczyn liczb pierwszych, i to tylko na jeden sposób. Matematycy chcą wiedzieć jak najwięcej o liczbach pierwszych – ta wiedza generuje wiedzę o wszystkich liczbach naturalnych. Wiadomo, że liczb pierwszych jest nieskończenie wiele. Udowodnił to już Euklides w słynnych „Elementach”. Niestety liczby pierwsze niechętnie poddają się badaniom. Choć wiemy, że jest ich nieskończenie wiele, to nie znamy żadnego wzoru, który by je generował. Ich rozmieszczenie na osi liczbowej też jest tajemnicą. Czasem liczby pierwsze występują tuż obok siebie – różnią się o 2, ale przerwy, gdzie nie ma liczb pierwszych, mogą być dowolnej długości. Duże liczby pierwsze znalazły ważne zastosowanie w teorii kodowania, w tzw. szyfrach z kluczem publicznym. Dlatego liczby pierwsze o dwustu i więcej cyfrach stały się towarem pożądanym i chronionym nie mniej niż największe tajemnice wojskowe. Problemem jest algorytm wyszukiwania liczb pierwszych, gdyż wszystkie znane algorytmy są bardzo wolne. Nawet bardzo szybkie komputery nie potrafią szybko rozkładać na czynniki wielkich liczb. Może na szczęście, gdyż znalezienie takiego skutecznego algorytmu spowodowałoby katastrofę w dziedzinie ochrony danych. Trzeba by szukać nowych metod szyfrowania [więcej o naturze liczb pierwszych pisze także Tomasz Miller].
Mimo kłopotów z algorytmami trwają polowania na wielkie liczby pierwsze. Na koniec 2017 r. największą była liczba 277232917-1. Można spokojnie ją zaliczyć do tych „praktycznie nieskończonych”. Ile ma cyfr? Naprawdę nietrudny rachunek (ale za pomocą tak nielubianych logarytmów) pokazuje, że rekordzistka ma dokładnie 23 249 425 cyfr. Nieprzypadkowa jest postać rekordzistki: 2p-1, gdzie p jest liczbą pierwszą. Liczby tej postaci nieco łatwiej poddają się testom na pierwszość. „Łatwiej” nie oznacza jednak, że prosto. Do badania tych liczb najpierw wykorzystywano superkomputery, a później sieci komputerów. Są to liczby nazywane liczbami Mersenne’a. Czytelnik być może się domyślił, że nie każda liczba tej postaci będzie liczbą pierwszą (inaczej mówienie o rekordach nie miałoby sensu). Na koniec listopada 2018 r. znanych jest 50 liczb pierwszych Mersenne’a i nie wiadomo, czy jest ich nieskończenie wiele, czy też istnieje wśród nich największa. Być może ktoś kiedyś wskaże ostatnią albo... udowodni, że takiej nie ma.
Książę amatorów
Z liczbami pierwszymi i olbrzymami związana jest jeszcze inna historia. Chodzi o liczby Fermata: dla każdej liczby naturalnej k można wskazać odpowiadającą jej liczbę F_k , wynoszącą 2 do potęgi 2^k , plus 1.
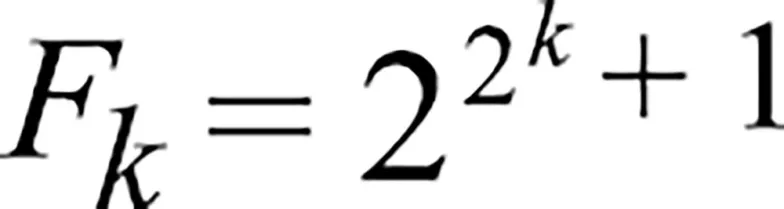
Pierre de Fermat, nazywany czasem księciem amatorów, postawił hipotezę, że być może liczby tej postaci są liczbami pierwszymi. Rzeczywiście F0=3, F1=5, F2=17, F3=257 i F4=65537 są pierwsze, ale F5= 232+1 już nie. Naturalne jest więc pytanie, które z liczb Fermata są jeszcze pierwsze. Pytanie jest zasadne, gdyż prawie 150 lat później okazało się, że liczby te mają ścisły związek z konstrukcjami wielokątów foremnych za pomocą cyrkla i linijki. Niestety do dziś nie znaleziono żadnej innej, poza wymienionymi, liczby pierwszej takiej postaci. Sprawdzono wszystkie liczby aż do F32 oraz sporo dalszych, już wyrywkowo. Największą znaną liczbą złożoną Fermata (na koniec listopada 2018) jest F3329780, która ma dzielnik 193 x 23329782 + 1. Zauważmy, że tego nie da się sprawdzić prosto za pomocą komputera, bowiem liczba jest już przeogromna. Tu potrzebna jest odrobina pomysłowości i szczęścia. Już sama liczba 23329780 budzi respekt, licząc blisko milion cyfr, a to ma się znaleźć w wykładniku innej potęgi dwójki. Podobnie jak w przypadku liczb Mersenne’a, nie wiemy, ile jest pierwszych liczb Fermata. Na razie żadnej nowej nie znamy. Nie wiemy także, ile jest takich liczb złożonych. Z pewnością jednych lub drugich jest nieskończenie wiele, tylko których? Może się też zdarzyć sytuacja trochę absurdalna, lecz nie niemożliwa: liczb pierwszych Fermata jest nieskończenie wiele, lecz żadnej z tych następnych nie będziemy w stanie opisać, nigdy!
W badaniach nad liczbami pierwszymi pojawiła się jeszcze jedna rekordzistka – tzw. liczba Skewesa, do której wygodnego zapisu potrzebujemy trzech „pięter” potęg. To 10 do potęgi, w której wykładniku mamy 10 do potęgi 10 do potęgi 34.
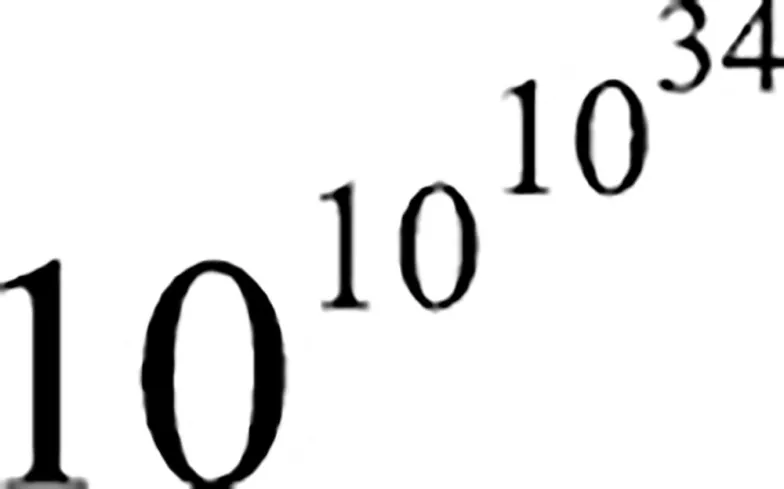
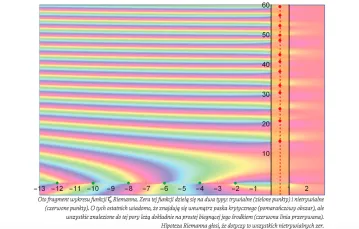
Ten dość niewinnie wyglądający zapis przedstawia olbrzyma przewyższającego zdecydowanie liczbę Archimedesa, liczbę jeszcze bardziej „praktycznie” nieskończoną niż te opisane wcześniej. Przypadek liczby Skewesa jest jednym z wielu przykładów pokazujących, że w matematyce, aby stwierdzić prawdziwość jakiejś hipotezy, nie wystarczy sprawdzić miliard, bilion czy nawet kwadrylion (1016) przypadków. Konieczny jest dowód dla wszystkich przypadków; jeden kontrprzykład obala całe twierdzenie.
Liczbę Skewesa otrzymano, badając różnicę pewnych dwóch funkcji przybliżających liczbę liczb pierwszych mniejszych od zadanej liczby [o funkcjach tego typu pisze też Tomasz Miller w przywołanym wyżej artykule na stronach niniejszego dodatku]. Takie funkcje są bardzo przydatne przy szacowaniu liczby liczb pierwszych w danym przedziale. Przypuszczano na podstawie konkretnych obliczeń, że różnica takich dwóch bardzo ważnych funkcji ma stały znak. Zaskoczeniem był dowód Johna Littlewooda z 1914 r., że ta różnica zmienia znak nieskończenie wiele razy. Matematyk nie wskazał jednak żadnej takiej wartości, dla której to ma miejsce. W 1933 r. Stanley Skewes udowodnił, że pierwsza zmiana znaku powinna nastąpić dla liczby mniejszej właśnie od liczby Skewesa. Rezultat kuriozalny, lecz w matematyce takie sytuacje są normalne. W przypadku omawianego problemu szacowanie udało się znacznie zmniejszyć i liczba Skewesa straciła swoje znaczenie. Znalazła jednak godną następczynię – liczbę Grahama.
Liczba Grahama pojawia się w teorii grafów, obecnie bardzo rozwijającej się i modnej ze względu na liczne, również praktyczne, zastosowania. Nie będziemy opisywać problemu, w którym pojawia się ta liczba, ale przyjrzymy się samej liczbie.
Matematycy mają swoje sposoby, żeby tworzyć liczby niewyobrażalnie wielkie. Jednym z nich jest tak zwana notacja Knutha. Umówmy się, że zamiast pisać na będziemy pisać n↑a, a gdy liczbę 10 chcemy podnieść do potęgi 1010, zapiszemy to 10↑10↑10. Idźmy dalej: zamiast m↑m↑...↑m napiszmy m↑↑n, gdy m powtarza się n razy, czyli naszą liczbę „10 podniesione do potęgi 1010” możemy zapisać w postaci 10↑↑3. To jednak nie koniec. Napiszemy m↑↑↑n, zamiast m↑↑m↑↑...↑↑m, gdzie... tak, tak, m powtarza się n razy. Podobnie definiujemy m↑↑↑↑n, m↑↑↑↑↑n, i tak dalej. Uprośćmy jeszcze zapis, żeby liczba strzałek się nie myliła. Mniej wygodny zapis m↑↑↑↑↑n zastąpmy prostszym m↑5n.
Teraz możemy w końcu opisać liczbę Grahama: konstruujemy liczby G1 = 3↑43, G2 = 3↑G13, G3 = 3↑G23, i tak 64 razy. Liczbę G64 nazywamy właśnie liczbą Grahama. To dopiero jest „praktyczna nieskończoność”, tu chyba żadna wyobraźnia nic nie pomoże. Już G1 jest, delikatnie mówiąc, monstrualnie wielka – choć do nieskończoności ciągle jej daleko.
Z takimi nieprawdopodobnie wielkimi liczbami w matematyce mamy do czynienia coraz częściej. Być może praca z nimi to przyszłość matematyki – lub jej znacznej części. Być może gdzieś tam niewyobrażalnie daleko odnajdziemy „proste” regularności pozwalające rozwiązać problemy typu ilości pierwszych liczb Mersenne’a, pierwszych liczb Fermata i wielu jeszcze innych. Być może. ©