Mistrz gry

Choć światek matematyków dzieli się na dziesiątki wąskich, specjalistycznych dziedzin, trudno znaleźć w nim kogoś, kto nie słyszałby o Johnie Conwayu. Jego idee i wyniki wywarły znaczący wpływ na teorię liczb i teorię gier, na geometrię, analizę i algebrę, a nawet na fizykę kwantową i teorię strun.

Jednak dla szerszego grona matematycznych pasjonatów jego postać zawsze będzie kojarzyć się głównie z całym mnóstwem gier i zagadek logicznych, w których wymyślanie i analizowanie Conway wciągnął się już na początku studiów w Cambridge. To pozornie niegroźne hobby wkrótce zaczęło graniczyć z obsesją, która odciągała go od nauki i znacznie wydłużyła jego studia doktoranckie. Przez wiele lat martwił się, że słabość do takich „niepoważnych” zagadnień ostatecznie zrujnuje mu karierę akademicką. Tymczasem właśnie ona zrodziła jego dwa największe odkrycia.

Pierwszym, z którego był najbardziej dumny, był nowy rodzaj liczb – tzw. liczby nadrzeczywiste (ang. surreal numbers). Z kolei największą sławę przyniosła mu „Gra w życie” („Game of Life”).

Arytmetyka nieskończoności

Współczesnych traktatów matematycznych raczej nie pisze się w formie dialogu. A jednak na taką właśnie formę zdecydował się informatyk Donald Knuth, pragnąc spopularyzować nowy system liczbowy opracowany przez Conwaya. Bohaterowie napisanej w tydzień i wydanej w 1974 r. powiastki pod tytułem „Surreal numbers. How two ex-students turned on to pure mathematics and found total happiness” („Liczby nadrzeczywiste. Jak dwoje eksstudentów zwróciło się ku czystej matematyce i odnalazło pełnię szczęścia”) natrafiają na wykutą w kamieniu staro­hebrajską inskrypcję zaczynającą się od słów: „Na początku wszystko było pustką, aż J.H.W.H. Conway jął stwarzać liczby”. Stylizowany na Księgę Rodzaju tekst najpierw opowiada, jak na bazie zbioru pustego zostało stworzone zero. Następnie zadaje regułę powstawania nowych liczb z tych skonstruowanych wcześniej, a także formułuje zręby arytmetyki („i widział, że były dobre”). Potem inskrypcja się urywa, a zaintrygowana para bohaterów przystępuje do samodzielnego dokończenia dzieła numerycznego stworzenia.

Początkowo wydaje się, że reguły Conwaya prowadzą po prostu do znanych ze szkoły liczb rzeczywistych. Oto w kolejnych krokach („dniach stworzenia”) stopniowo wyłaniają się liczby całkowite, a przestrzeń między nimi coraz gęściej wypełniają ułamki. Po nieskończonej liczbie kroków („w dniu omega”) bohaterowie potrafią już skonstruować każdą liczbę – zarówno wymierną, jak i niewymierną. Ze zdziwieniem odkrywają jednak, że w istocie otrzymali znacznie więcej, albowiem przepis Conwaya niejako mimochodem generuje także liczby „pozaskończone” oraz „infinitezymalne”, czyli odpowiednio większe i mniejsze od wszystkich dodatnich liczb rzeczywistych. Choć takie nieskończenie wielkie i nieskończenie małe obiekty były już wcześniej znane matematykom, to nie tworzyły tak wszechogarniającego, arytmetycznie spójnego systemu, w którym nieskończoności można nie tylko porównywać, dodawać i mnożyć (to potrafił już w XIX w. twórca teorii mnogości Georg Cantor), ale też odejmować i dzielić, a nawet pierwiastkować i logarytmować.

Czytaj także: Tomasz Miller: Geniusz bez doktoratu

Mimo upływu niemal pół wieku o liczbach nadrzeczywistych wciąż wiemy stosunkowo niewiele. Sam Conway liczył, że okażą się przydatne w fizyce fundamentalnej, ale na razie ich zastosowanie właściwie nie wykracza poza tzw. kombinatoryczną teorię gier, w kontekście której zostały odkryte. Wszystko zaczęło się bowiem od tego, że pod koniec lat 60. Conway z ciekawości analizował… końcowe warianty partii go, czyli starochińskiej gry planszowej porównywanej (niezbyt celnie) do szachów.

Życie na szachownicy

Mniej więcej w tym samym czasie Conway – również za pomocą planszy i kamieni do go – dokonał swojego drugiego największego odkrycia. Dotyczyło ono tzw. „automatów komórkowych”, wymyślonych kilkanaście lat wcześniej przez Johna von Neumanna i Stanisława Ulama.

Aby zrozumieć, czym jest automat komórkowy, wyobraźmy sobie świat jako wielką szachownicę. W świecie tym czas jest podzielony na tury. Każde kwadratowe pole – zwane „komórką” – może znajdować się w jednym z kilku stanów. Stan komórki może się zmieniać z tury na turę, przy czym to, czy tak się stanie, jest w całości zdeterminowane przez stan ośmiu sąsiednich komórek, zgodnie z pewnymi przyjętymi na początku regułami. Właśnie dlatego mówimy o „automacie” albo o „grze dla zera graczy”. Rola gracza ogranicza się bowiem wyłącznie do wyboru początkowego stanu poszczególnych komórek – potem gra toczy się już sama.

Von Neumann i Ulam badali automaty komórkowe, które miały zdolność samopowielania lub symulowały pewne zjawiska fizyczne, takie jak ruch płynu. Conway był zainteresowany czymś innym – szukał możliwie najprostszych reguł, które prowadziłyby do zróżnicowanego, nieprzewidywalnego zachowania. Nie dysponując z początku maszyną liczącą, skupił się na komórkach o zaledwie dwóch możliwych stanach: „żywa” i „martwa”, umieszczając i zdejmując kamienie do go zgodnie z różnymi zestawami reguł. Po wielu miesiącach eksperymentów odkrył trzy zasady, które nie tylko zapewniały subtelną równowagę między życiem a śmiercią, ale także prowadziły do zaskakującego bogactwa form, przywodzącego na myśl kolonie mikroorganizmów, które rosną, przemieszczają się, dzielą i umierają.

Tak narodziła się „Gra w życie”. Spopularyzowana w felietonie legendarnego Martina Gardnera na łamach „Scientific American”, natychmiast stała się przebojem. Nieliczni szczęśliwcy, którzy mieli dostęp do maszyn liczących, godzinami wpatrywali się w walkę o pikselowy byt. Jak głosi legenda, w latach 70. nawet jedna czwarta wszystkich komputerów świata (wliczając maszyny wojskowe), pokątnie grała w Conwayową „Grę” za sprawą urzeczonych nią programistów. Niczym egzotyczną faunę i florę, odkrywano i klasyfikowano coraz to nowe układy stabilne (still life), okresowe (oscillators), przemieszczające się (spaceships) albo zdolne wytwarzać inne układy (guns, puffers, rakes). W 1982 r. ­Conway udowodnił, że wewnątrz „Gry” teoretycznie możliwe jest skonstruowanie tzw. uniwersalnej maszyny Turinga, czyli komputera realizującego dowolny algorytm. W tego typu maszynie do przesyłania zero-jedynkowych sygnałów można wykorzystać tzw. glidery, a w roli twardych dysków – proste układy stabilne. Komputer taki udało się zresztą skonstruować w 2000 r. i do dziś „inżynierowie życia” dokonują w nim kolejnych usprawnień.

„Gra w życie” wywarła głębokie wrażenie nie tylko na matematykach i infor­matykach. Ponieważ dostarcza uderzającego przykładu samoorganizacji i emergencji, bywa wykorzystywana przez fizyków, biologów, ekonomistów, a nawet badaczy umysłu jako ilustracja wyłaniania się złożonych zjawisk i zachowań z kilku prostych, niepozornych zasad.

Epilog

John Horton Conway zmarł nagle 11 kwietnia 2020 r. w wyniku komplikacji związanych z COVID-19, raptem trzy dni po pojawieniu się pierwszych objawów choroby. Miał 82 lata.

Randall Munroe, autor popularnego komiksu internetowego „xkcd”, stworzył krótką animację-hołd dla genialnego matematyka. Widać na niej ludzką sylwetkę zbudowaną z 21 kwadratów, która nagle przeobraża się w pojedynczy glider ulatujący poza prawą górną krawędź planszy. Wszystko zgodnie z nieubłaganymi regułami gry w życie. ©

Reguły życia i śmierci

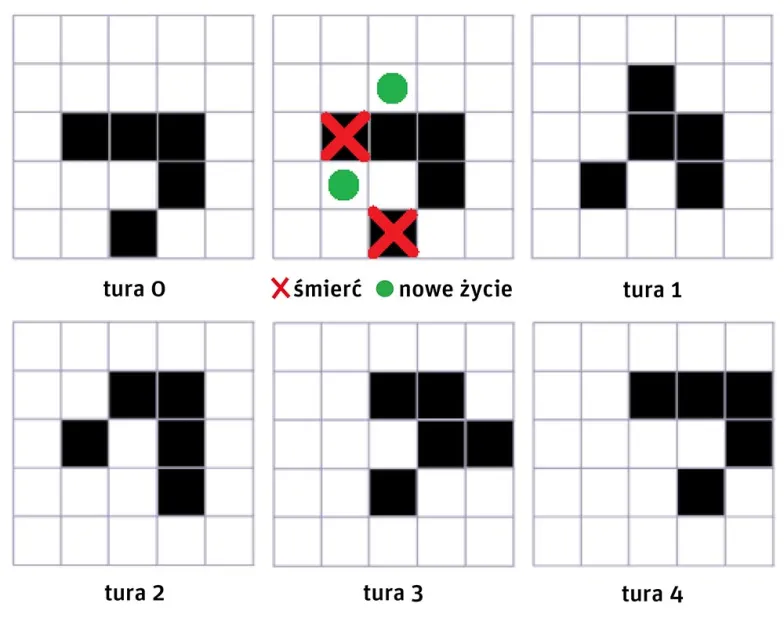
Żywa komórka (kolor czarny), która sąsiaduje z mniej niż dwoma żywymi komórkami, umiera z samotności.

Żywa komórka, która sąsiaduje z więcej niż trzema żywymi komórkami, umiera z przeludnienia.

Martwa komórka (kolor biały), która sąsiaduje z dokładnie trzema żywymi komórkami, ożywa.

„Sąsiaduje” oznacza „styka się bokiem lub wierzchołkiem”. W przypadkach nieuwzględnionych powyżej komórka nie zmienia swojego stanu. Ilustracja przedstawia tzw. glider, będący najprostszym układem przemieszczającym się. Co cztery tury powraca on do pierwotnej konfiguracji, tyle że przesuniętej do góry i w prawo.