Wykupienie dostępu pozwoli Ci czytać artykuły wysokiej jakości i wspierać niezależne dziennikarstwo w wymagających dla wydawców czasach. Rośnij z nami! Pełna oferta →
Jak napisał w znanym podręczniku analizy matematycznej Krzysztof Maurin: "z podziałem na klasy [jedną z podstawowych operacji matematycznych] wiąże się jedna z najciekawszych własności umysłu ludzkiego: zdolność abstrahowania, polegająca na tym, że pomija się różnice między elementami tej samej klasy, a klasy ujmuje się jako nowe indywidua (»abstrahuje się od różnic indywidualnych«). Na pierwszy rzut oka zdawałoby się, że abstrahowanie zuboża świat pojęć, lecz jest właśnie przeciwnie...".
Stary spór o to, czy matematycy wynajdują, czy odkrywają obiekty matematyczne, jest chyba dobrze rozstrzygnięty (choć nie wszyscy się z tym zgodzą) w słynnym zdaniu Leopolda Kroneckera: "liczby naturalne stworzył dobry Bóg, reszta jest dziełem człowieka". Ale jeśli zastanowić się, co to jest liczba, to okaże się, że jest rezultatem abstrahowania, o którym mówił Maurin: cztery śliwki, cztery konie i cztery gwiazdy mają coś wspólnego, choć są czymś zupełnie innym.
Wyjątkowość matematyki jako dziedziny kultury polega też na tym, że nie sposób podać jej definicji. W trzynastotomowej encyklopedii PWN hasło "matematyka" zaczyna się od zdania: "obecnie łamie ramy wszelkich definicji wytyczających przedmiot jej badań. Nie udało się dotąd znaleźć określenia, które charakteryzowałoby matematykę w pełni i zadowalało choćby samych tylko matematyków". Britannica wyjaśnia, że matematyka to "nauka o strukturze, porządku i relacjach, która wyewoluowała z podstawowych praktyk liczenia, mierzenia i opisu kształtów przedmiotów". Od takich praktyk matematyka oderwała się niemal całkowicie i dziś jej jedynym kontaktem ze "sferą realną" wydają się być właśnie kroneckerowskie liczby naturalne.
Tym bardziej zdumiewa, że matematyka dostarcza najlepszego znanego języka, w którym wyrażane są podstawowe prawa przyrody. Niektóre prawa zostały wręcz odkryte nie w drodze doświadczeń czy obserwacji, ale badania struktur matematycznych! I choć fizyka to nie tylko matematyka, a matematyka wydaje się być pojemniejsza niż rzeczywistość materialna, to nie sposób wyobrazić sobie współczesnych nauk przyrodniczych bez matematyki.
Większości ludzi matematyka kojarzy się z prostymi rachunkami, z elementarną arytmetyką, z tym, co sprzedawca w warzywniaku notuje długopisem na szarej papierowej torebce albo księgowy w firmie na kalkulatorze. Autystyczne zdolności do mnożenia w pamięci wielkich liczb bywają przedstawiane w mediach jako "zdolności matematyczne". Nawet szkolne funkcje i algebra do współczesnej matematyki mają się jednak tak, jak znajomość abecadła do głębokiej kultury filologicznej.
Zrozumienie, czym naprawdę jest matematyka, mogłaby umożliwić dobra jej popularyzacja. O to jednak niełatwo. Abstrakcyjny charakter matematyki sprawia, że popularyzować ją o wiele trudniej niż inne dziedziny nauk przyrodniczych czy historię sztuki. Fizyk zawsze może się odwoływać do analogii z otaczającego nas świata (choć w przypadku mechaniki kwantowej to już zawodzi). Historyk sztuki może pokazać reprodukcje dzieła, muzyk - odtworzyć fragment utworu. Matematyk musi odwołać się do wyobraźni i zdolności do abstrahowania - a z tym bywa różnie.
W Polsce książki popularyzujące matematykę ukazują się rzadko. Na szczęście te, które są wydawane, bywają znakomite. Z dzieciństwa pamiętam "Zygzakiem przez matematykę" Wojciecha Bieńki, "Co to jest matematyka" Richarda Couranta i Herberta Robbinsa, "Kalejdoskop matematyczny" Hugona Steinhausa czy piękną "Apologię matematyka" G.H. Hardy’ego. Już na studiach czytywałem znakomite artykuły popularne w miesięczniku "Delta". Kilka lat temu ukazały się piękne książki Krzysztofa Ciesielskiego i Zdzisława Pogody "Bezmiar matematycznej wyobraźni" i "Diamenty matematyki" oraz "Matematyka przy kominku" Michała Szurka. Pewnie było ich więcej.
Paweł Strzelecki, autor "Matematyki współczesnej dla myślących laików", jest matematykiem na Uniwersytecie Warszawskim. Od lat popularyzuje matematykę artykułami w "Delcie", wykładami na Festiwalach Nauki, na Uniwersytecie Dzieci i przekładami. W działalności popularyzatorskiej łączy sympatię i wyrozumiałość dla odbiorcy z zawodową pasją i bezkompromisowością, polegającą na nieunikaniu trudnych spraw. Popularyzacja - tak, ale tam, gdzie prościej się już nie da, nie wolno iść na skróty. W pełni podzielam takie podejście.
"Matematyka" Strzeleckiego jest w zamyśle podobna do książki Couranta i Robbinsa sprzed niemal pięćdziesięciu lat. Ten przedział czasu oznacza jednak wielkie zmiany i rozwój w matematyce. Autor chce wprowadzić nas w świat matematyki najbardziej współczesnej, czytamy tu o osiągnięciach dosłownie sprzed kilku lat. Najbardziej pasjonujący, choć chyba najmniej szczegółowy i najbardziej "popularyzatorski" (bez wchodzenia w szczegóły, których w takim ujęciu i takiemu odbiorcy nie da się przedstawić), jest ostatni rozdział książki: "Katalog kształtów naszego Wszechświata". Dotyczy on dowodu hipotezy Poincarégo, przeprowadzonego przez rosyjskiego matematyka Grigorija Perelmana. Ten geniusz z Petersburga stał się sławny w mediach głównie z powodu ekscentrycznego zachowania (np. odmowy przyjęcia Medalu Fieldsa - matematycznego Nobla). Strzelecki stanowczo i jasno wyjaśnia, że nie chodzi tu ani o wariata, ani o efekciarstwo, ale o najgłębiej rozumianą naukową uczciwość i czystość Perelmana.
"Matematyka współczesna dla myślących laików" zaczyna się rozdziałem o liczbach - i słusznie, bo jeśli matematyka jest królową nauk, to teoria liczb jest królową matematyki. Z wielką przyjemnością czytałem ten rozdział; jeszcze jako uczeń dostałem od ojca pierwszy prawdziwy podręcznik akademicki i była to "Arytmetyka teoretyczna" Wacława Sierpińskiego, tom siódmy wspaniałej serii Biblioteka Matematyczna. Rozdziały kolejne, a jest ich w sumie dziewięć, przynoszą przegląd wybranych problemów matematyki współczesnej. Pomimo zastrzeżenia autora, że książka nie ma być kompletną prezentacją tej dziedziny, wybrane tematy są dość szerokie.
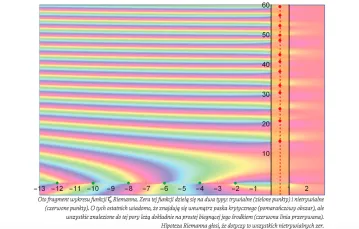
Obraz matematyki, jaki się z niej wyłania, jest zachwycający i wciągający. Fraktale, funkcja ? Riemanna, współczesna kryptografia, komórki Woronoja... Książka jest o matematyce współczesnej, ale jej osnowę stanowią stare problemy, stare hipotezy. Niektóre z nich zostały rozstrzygnięte niedawno właśnie przy pomocy najnowocześniejszych matematycznych środków. Inne wciąż czekają na geniuszy pokroju Perelmana.
Książka Strzeleckiego jest piękną popularyzacją matematyki. Autor nie ulega pokusie pokornego uzasadniania, dlaczego należy uprawiać matematykę. Nie przekonuje, że bez niej ani komputery, ani satelity, ani telefony komórkowe, ani bankomaty, ani inne potrzebne i niepotrzebne gadżety by nie działały - choć to akurat prawda. Tylko od czasu do czasu pokazuje znaczenie praktyczne osiągnięć matematycznych. Matematyka jest bowiem czymś więcej niż "zaawansowana hydraulika". Uprawia się ją z innych powodów. Niemal świętych. I o tym właśnie jest ta książka.
Nie ma co ukrywać: matematyka nie jest łatwa. Anegdota mówi, że kiedy rektor uniwersytetu w Getyndze, obserwując matematyka Hermana Weyla spacerującego całymi dniami w parku, zapytał go, dlaczego nie pracuje, usłyszał: "Panie rektorze, matematyka jest nauką tak trudną, że można się nią zajmować najwyżej pół godziny dziennie". Stefan Banach powiedział kiedyś do Hugona Steinhausa: "Wisz bracie, co ci powiem? Humanistyka jest w szkole ważniejsza od matematyki - matematyka to jest za ostry instrument, to nie dla dzieci...". Izaak Walton (1593-1683) pisał zaś: "Wędkarstwo jest jak matematyka, nigdy nie da się go w pełni nauczyć".
Czemu więc próbować, choćby czytając takie książki jak "Matematyka współczesna dla myślących laików"? Jak pisał Francis Bacon: "historia czyni człowieka mądrym, poezja dowcipnym, matematyka subtelnym...". A Stanisław Brzozowski tłumaczył: "Wy nie wiecie, co to jest matematyka! Wy myślicie: liczby, liczby! A ona śpiewa jak kryształ. Cała dusza tonie w dźwięcznym, przejrzystym krysztale".
Paweł Strzelecki, Matematyka współczesna dla myślących laików
Warszawa 2011, Wydawnictwa Uniwersytetu Warszawskiego.